FlashAttentionV1V2原理及代码学习

2024-09-01

FlashAttention是目前LLM推理最常用的Attetion算子实现框架，广泛使用在了vLLM, TensorRT-LLM中，本文是笔者关于FlashAttention的学习笔记，水平有限，如果有理解错误的地方也请指出。

参考材料

FlashAttention-V1论文: FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

FlashAttention-V2论文: FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning

From Online Softmax to FlashAttention

从Online-Softmax到FlashAttention V1/V2/V3

FlashAttention:加速计算,节省显存, IO感知的精确注意力

背景及动机

从论文题目可以看出，FlashAttentionV1工作通过IO-Awareness技术：

Fast: 加速了Attention的计算过程
Memory-Efficient: 优化了Attention计算过程中的显存使用
Exact Attention: 精确Attention计算结果，和标准Attention计算结果相同
FlashAttentionV2工作主要是在V1上优化了并行和Work划分。

标准Attention的计算公式如下：

$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d}})V$

上面的计算可以分为三个部分:

$S=QK^T \in R^{N \times N}$
$P=softmax(S) \in R^{N \times N}$
$O=PV \in R^{N \times d}$

计算过程图示及算法伪代码如下：
6de03ee4e0d1205c40b19fe2de000065

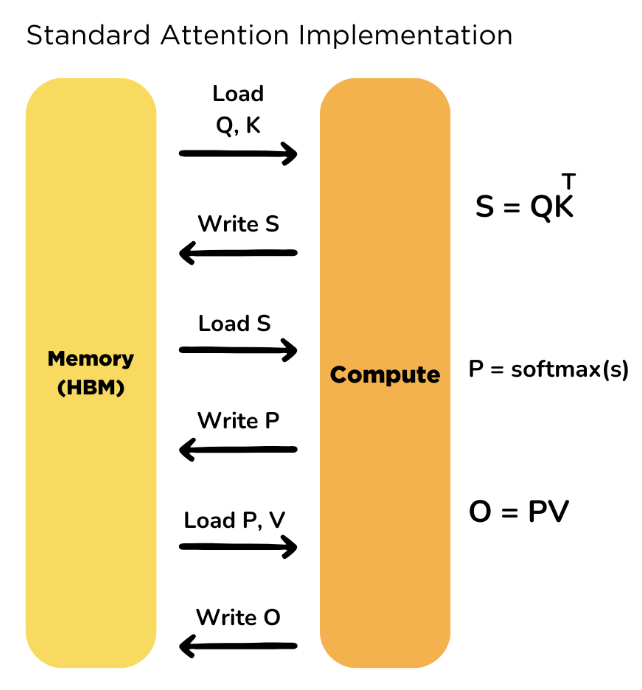
500cb07d49a66e71bd5c29a333ef3d8d

上面的计算过程有两个缺点：

显存占用多，中间计算结果矩阵$S,P \in R^{N \times N}$导致了$O(N^2)$的显存占用，通常来说，$N >> d$
大量的HBM的读写操作，HBM的带宽很低，会导致整个计算过程变慢

GPU内存分层：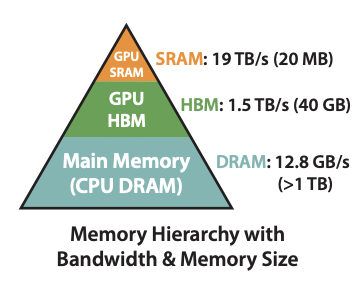
382ecb5b01b53022b959dfa5b6986c10

FlashAttention V1 V2优化

对比标准Attention的实现，flash attention 的核心思路是通过分块计算，将中间计算 fuse 在一起，避免来回读写中间，减少访问 HBM 的次数，提高计算效率。具体如下：

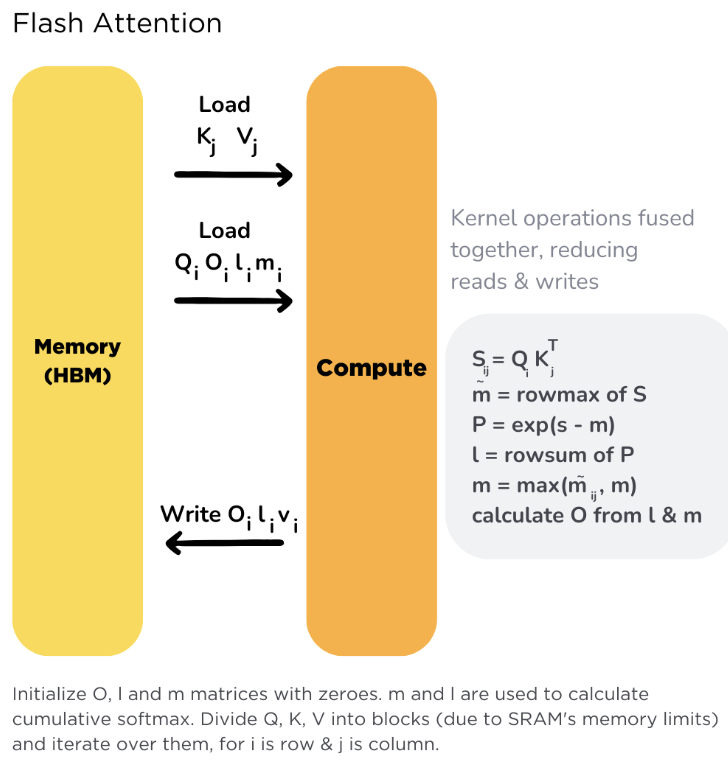
5656de87950d649195e6db9b2b0614b1

1. Tiling: 矩阵乘法，具有分块和累加的特性，一个大的矩阵乘法，可以通过Tiling技术，分成小块加载到高速的SRAM完成计算，然后通过将各个分块矩阵乘的结果进行累加获得最后的正确结果，减少HBM的总访存量。tiling技术在矩阵乘法GEMM算子实现中都会用到。
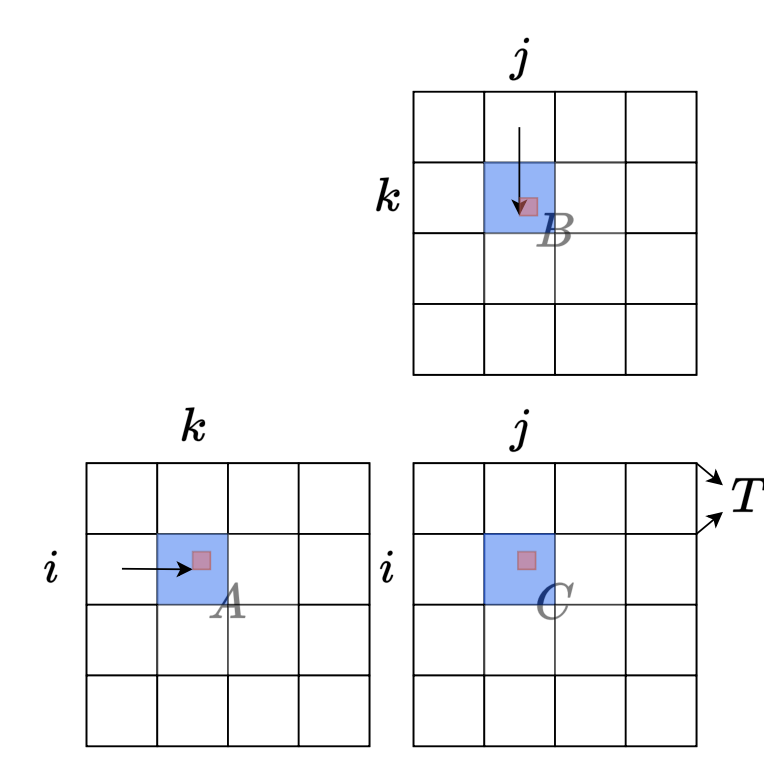
4a5a8667d9c8693e25678f043ba94e32
想了解GEMM优化的同学可以看下面的材料，感觉都写的挺好的：
深入浅出GPU优化系列：GEMM优化（一）

online-softmax: 遗憾的是，Attention计算过程除了矩阵乘法以外，主要问题是有个Softmax的分母项依赖于全局的一行输入，也就是说$P_i=softmax(Q_iK^T)$依赖$Q_i$矩阵块与整个$K^T$矩阵完成计算。FlashAttention和online softmax想解决的核心问题，正是如何将算法本身从这个全局的依赖中解耦，从而可以使用Tiling进行快速的片上计算

Online Softmax个人理解：

我们想计算一个$X \in R^{BT}$上的$softmax$分布, 表达式如下：

$softmax(X) = \frac {e^{x^i-m}} {\sum_{i=1}^{B*T}{e^{x^i-m}}}$

其中，m=max(X), 减去m是为了防止指数运算溢出(safe softmax实现)。

假如我们开了天眼，已经知道全局的$m=max(X)$，和$l=\sum_{i=1}^{B*T}{e^{x^i-m}}$，那么softmax过程可以拆分为：

$softmax(X) = \sum_{i=1}^{T}{\frac{exp(X_{T_i}-m)}{l}}$

其中，$X$被分为$T$个小块，$X_{T_i} \in R^{B}$。这样看着可以完成tiling计算的需求。

但是我们目前没有天眼的，只能知道所有已计算过的分块中$m$，以及$l$, 即：

分块1:
$softmax(X_{T_1})=\frac {exp(X_{T_1}-m_1)}{l_1}$
$m_1 = max(X_{T_1})$
$l_1=sum(exp(X_{T_1}-m_1))$
分块2:
$softmax(X_{T_2})=\frac {exp(X_{T_2}-m_2)}{l_2}$
$m_2 = max(m_1, rowmax(X_{T_2}))$
$l_2=sum(exp(X_{T_1,T_2}-m_2))={l_1}e^{m_1 - m_2}+sum(exp(X_{T_2}-m_2)$
$softmax(X_{T_1,T_2})=\frac{l_1}{l_2} softmax(X_{T_1}) e^{m_1 - m_2}+softmax(X_{T_2})$
….
分块T:
$softmax(X_{T_T})=\frac {exp(X_{T_T}-m)}{l}$
$m = m_T = max(m_{T-1}, rowmax(X_{T_T}))$ 得到了前面开天眼的l和m
$l = l_T =sum(exp(X-m))={l_{T-1}}e^{m_{T-1} - m}+sum(exp(X_{T_{T}}-m)$
$softmax(X)=\frac{l_{T-1}}{l} softmax(X_{T_1,….T_T-1}) e^{m_{T-1} - m}+softmax(X_{T_T})$

这样分块迭代是可以满足tiling要求，并计算出精确的softmax的，可以对着下面算法伪代码看，流程是一样的：
7007bd678bb94297f2fc42d9fa508a4b

唯一区别是，softmax中间存放的结果是$exp(X_{T_1}-m_1)$这种格式，把每次除l的放缩部分拿最后算了，这样可以进一步加速。

Triton源码学习

代码来源：Fused Attention

FlashAttention仓库内容太多了，Triton实现比较精简，更容易阅读

@triton.jit
def _attn_fwd_inner(acc, l_i, m_i, q,  #
                    K_block_ptr, V_block_ptr,  #
                    start_m, qk_scale,  #
                    BLOCK_M: tl.constexpr, HEAD_DIM: tl.constexpr, BLOCK_N: tl.constexpr,  #
                    STAGE: tl.constexpr, offs_m: tl.constexpr, offs_n: tl.constexpr,  #
                    N_CTX: tl.constexpr, fp8_v: tl.constexpr):
    # 计算softmax(Q_i*K)V
    # range of values handled by this stage
    if STAGE == 1:
        lo, hi = 0, start_m * BLOCK_M
    elif STAGE == 2:
        lo, hi = start_m * BLOCK_M, (start_m + 1) * BLOCK_M
        lo = tl.multiple_of(lo, BLOCK_M)
    # causal = False
    else:
        lo, hi = 0, N_CTX
    K_block_ptr = tl.advance(K_block_ptr, (0, lo))
    V_block_ptr = tl.advance(V_block_ptr, (lo, 0))
    # loop over k, v and update accumulator
    # 这里步骤和伪代码中步骤一致
    for start_n in range(lo, hi, BLOCK_N):
        start_n = tl.multiple_of(start_n, BLOCK_N)
        # -- compute qk ----
        k = tl.load(K_block_ptr)
        qk = tl.dot(q, k)
        if STAGE == 2:
            mask = offs_m[:, None] >= (start_n + offs_n[None, :])
            qk = qk * qk_scale + tl.where(mask, 0, -1.0e6)
            m_ij = tl.maximum(m_i, tl.max(qk, 1))
            qk -= m_ij[:, None]
        else:
            m_ij = tl.maximum(m_i, tl.max(qk, 1) * qk_scale)
            qk = qk * qk_scale - m_ij[:, None]
        p = tl.math.exp2(qk)
        l_ij = tl.sum(p, 1)
        # -- update m_i and l_i
        alpha = tl.math.exp2(m_i - m_ij)
        l_i = l_i * alpha + l_ij
        # -- update output accumulator --
        acc = acc * alpha[:, None]
        # update acc
        v = tl.load(V_block_ptr)

        p = p.to(tl.float16)
        acc = tl.dot(p, v, acc)
        # update m_i and l_i
        m_i = m_ij
        V_block_ptr = tl.advance(V_block_ptr, (BLOCK_N, 0))
        K_block_ptr = tl.advance(K_block_ptr, (0, BLOCK_N))
    return acc, l_i, m_i


@triton.autotune(list(filter(keep, configs)), key=["N_CTX", "HEAD_DIM"])
@triton.jit
def _attn_fwd(Q, K, V, sm_scale, M, Out,  #
              stride_qz, stride_qh, stride_qm, stride_qk,  #
              stride_kz, stride_kh, stride_kn, stride_kk,  #
              stride_vz, stride_vh, stride_vk, stride_vn,  #
              stride_oz, stride_oh, stride_om, stride_on,  #
              Z, H, N_CTX,  #
              HEAD_DIM: tl.constexpr,  #
              BLOCK_M: tl.constexpr,  #
              BLOCK_N: tl.constexpr,  #
              STAGE: tl.constexpr  #
              ):
    tl.static_assert(BLOCK_N <= HEAD_DIM)
    # grid并行参数 <<< N/B_M, Z*H, 1 >>> 在seq_len (query), batch_size, heads三个纬度上做并行
    # 每个Block需要完成softmax(Q_i,K)V这部分计算任务
    start_m = tl.program_id(0) #属于Q中哪个Q_i
    off_hz = tl.program_id(1) #ZH编号，指定是哪个Q
    off_z = off_hz // H
    off_h = off_hz % H
    #找到QKV矩阵的位置
    qvk_offset = off_z.to(tl.int64) * stride_qz + off_h.to(tl.int64) * stride_qh

    # block pointers
    # Q_i对应的矩阵内存分布
    Q_block_ptr = tl.make_block_ptr(
        base=Q + qvk_offset,
        shape=(N_CTX, HEAD_DIM),
        strides=(stride_qm, stride_qk),
        offsets=(start_m * BLOCK_M, 0),
        block_shape=(BLOCK_M, HEAD_DIM),
        order=(1, 0),
    )
    v_order: tl.constexpr = (0, 1) if V.dtype.element_ty == tl.float8e5 else (1, 0)
    # V对应的矩阵内存分布
    V_block_ptr = tl.make_block_ptr(
        base=V + qvk_offset,
        shape=(N_CTX, HEAD_DIM),
        strides=(stride_vk, stride_vn),
        offsets=(0, 0),
        block_shape=(BLOCK_N, HEAD_DIM),
        order=v_order,
    )
    # K对应的矩阵内存分布
    # K读取的order和shape反了一下
    K_block_ptr = tl.make_block_ptr(
        base=K + qvk_offset,
        shape=(HEAD_DIM, N_CTX),
        strides=(stride_kk, stride_kn),
        offsets=(0, 0),
        block_shape=(HEAD_DIM, BLOCK_N),
        order=(0, 1),
    )
    # O对应的矩阵分布
    O_block_ptr = tl.make_block_ptr(
        base=Out + qvk_offset,
        shape=(N_CTX, HEAD_DIM),
        strides=(stride_om, stride_on),
        offsets=(start_m * BLOCK_M, 0),
        block_shape=(BLOCK_M, HEAD_DIM),
        order=(1, 0),
    )
    # initialize offsets
    offs_m = start_m * BLOCK_M + tl.arange(0, BLOCK_M)
    
    offs_n = tl.arange(0, BLOCK_N)
    # initialize pointer to m and l
    m_i = tl.zeros([BLOCK_M], dtype=tl.float32) - float("inf")
    l_i = tl.zeros([BLOCK_M], dtype=tl.float32) + 1.0
    acc = tl.zeros([BLOCK_M, HEAD_DIM], dtype=tl.float32)
    # load scales
    qk_scale = sm_scale
    qk_scale *= 1.44269504  # 1/log(2)
    # load q: it will stay in SRAM throughout
    q = tl.load(Q_block_ptr)
    # stage 1: off-band
    # For causal = True, STAGE = 3 and _attn_fwd_inner gets 1 as its STAGE
    # For causal = False, STAGE = 1, and _attn_fwd_inner gets 3 as its STAGE
    # Casual情况为了减少计算量：
    #   对于i<j的部分，理论上是不需要计算的，通过下面的区分是为了节约部分计算量
    # stage&1部分完全满足计算i<j的部分
    # stage&2部分计算i，j有重叠的部分，即Q_i中有元素索引<K_j中索引，有的又大于
    if STAGE & 1:
        acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr,  #
                                        start_m, qk_scale,  #
                                        BLOCK_M, HEAD_DIM, BLOCK_N,  #
                                        4 - STAGE, offs_m, offs_n, N_CTX, V.dtype.element_ty == tl.float8e5  #
                                        )
    # stage 2: on-band
    if STAGE & 2:
        # barrier makes it easier for compielr to schedule the
        # two loops independently
        acc, l_i, m_i = _attn_fwd_inner(acc, l_i, m_i, q, K_block_ptr, V_block_ptr,  #
                                        start_m, qk_scale,  #
                                        BLOCK_M, HEAD_DIM, BLOCK_N,  #
                                        2, offs_m, offs_n, N_CTX, V.dtype.element_ty == tl.float8e5  #
                                        )
    # epilogue
    m_i += tl.math.log2(l_i)
    acc = acc / l_i[:, None]
    m_ptrs = M + off_hz * N_CTX + offs_m
    tl.store(m_ptrs, m_i)
    tl.store(O_block_ptr, acc.to(Out.type.element_ty))



class _attention(torch.autograd.Function):
    # q,k,v shape Z(batch_size), H(heads_num), N_CTX(seq_len), HEAD_DIM(h)
    @staticmethod
    def forward(ctx, q, k, v, causal, sm_scale):
        # shape constraints
        HEAD_DIM_Q, HEAD_DIM_K, HEAD_DIM_V = q.shape[-1], k.shape[-1], v.shape[-1]
        o = torch.empty_like(q)
        stage = 3 if causal else 1

        # grid并行参数 <<< N/B_M, Z*H, 1 >>> 在seq_len (query), batch_size, heads三个纬度上做并行  
        grid = lambda args: (triton.cdiv(q.shape[2], args["BLOCK_M"]), q.shape[0] * q.shape[1], 1)
        # [batch_size, heads_num, n]shape的m，和伪代码中m一样，不过是多了batch_size, heads_num两个纬度
        M = torch.empty((q.shape[0], q.shape[1], q.shape[2]), device=q.device, dtype=torch.float32)
        _attn_fwd[grid](
            q, k, v, sm_scale, M, o,  #
            q.stride(0), q.stride(1), q.stride(2), q.stride(3),  #
            k.stride(0), k.stride(1), k.stride(2), k.stride(3),  #
            v.stride(0), v.stride(1), v.stride(2), v.stride(3),  #
            o.stride(0), o.stride(1), o.stride(2), o.stride(3),  #
            q.shape[0], q.shape[1],  #
            N_CTX=q.shape[2],  #
            HEAD_DIM=HEAD_DIM_K,  #
            STAGE=stage,  #
            **extra_kern_args)
        return o

attention = _attention.apply